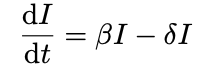Feb 19, 2021 | Fun
The Lebow Oratorical Competition has been a cornerstone tradition of the Pingry Upper School for decades. Unfortunately, its final round, which gets most of the attention, only as room for six speakers – which leaves many well-written speeches from the first round without an audience. As such, The Record has decided to reach out to speakers from the first round and give them the chance to publish excerpts from their speeches. Below are four excerpts we received:
Margaret Zachary
But the point stands that a small moment I had during my time abroad is what had the biggest impact on me. A short conversation with a handful of Iraqi refugees completely changed my view of the world so that I could be more aware of the struggles outside of my immediate community. A lesson on humanity all encompassed in a five-minute conversation. So, take note of the small interactions you have with people, the quick conversations, they might end up making an impact on you more than you think. Live your five-minute moments.
Herbert Toler
During the winter break, my family and I watched Toy Story 4. It was a refreshing opportunity because this family comedy series has been a staple of my youth.
As the latest installment of the series began, I felt concerned that I might have aged out of the content that I had loved in boyhood. Quickly, I realized this to be untrue. Soon we were introduced to Duke Kaboom, a new character that reminded me of the value of building community.
Throughout the film’s plot, I recognized how building community allowed for greater achievement, a sense of purpose, and a better understanding of each other.
While we may not live in a toy universe, make it your mission to care for those in our community, enabling us to reach our fullest potentials.
Today, I am calling for you to utilize the best resources we have available to us, each other.
Emma Drzala
Success is ultimately winning. Winning is whatever you want to define it as, but in the end, a winner is someone who has endured the hard moments, someone who has looked past the failures to reach their goals. Our teachers in High School always remind us that there is more to life than the gradebook, that High School is a small part in the puzzle that is life. Like most, I had–and still sometimes have–trouble accepting this notion. Losing occasionally can help us to realize this. Whether it be getting onto a team or getting admitted into college, everything we do seems to be for an end goal. My losses have shown me what I find most important in life, and I was finally motivated to succeed for myself, not for my end goal.
Zala Bhan
As someone who learned early on in life that communities don’t thrive if some are left behind, I find it unconscionable that some Americans have to choose between food, medicine, and the internet for their children to learn. […] Millions of kids, I remind you, of lower socio-economic backgrounds, primarily black and brown, are without proper access to basic schooling [during this time], and this is not a headline? […] We cannot live with this inequity, sitting safely guarded behind our plexiglass shields, while the academic pandemic throws some of our generation behind.

Feb 19, 2021 | Fun
By Hansen Zhang (III)
In 2021, Generation Z, or GenZ for short, is between 8 and 24 years old. It is fairly obvious that what separates our generation from all that have before us in human history is the fact that we have had the World Wide Web and social media at our fingertips from a young age. It is why we use the Internet more than other generation. According to a fact sheet by Pew Research Center in 2019, 90 percent of younger Americans (i.e. GenZ and Millennials) have used the Internet.
The GenZ sense of humor, as shown and archived through memes, is also distinct in its absurdity and randomness. It is natural to ask: Why are GenZ memes so absurd, so “spicy” and “dank”? To be honest, I do not believe there is a clear reason. People have simply found out that random things are funny. The punchline of the random meme is precisely that it just doesn’t make sense; it’s ironically funny. It’s like you’re watching a basketball game where the players are all air balling their shots. It shouldn’t be entertaining, but it is.
As with many things, there is a dark side to GenZ humor. Memes regarding depression or uncertainty about the future are very prevalent on social media. If you browse a meme-related Reddit Community, you’ll probably be able to find a depression-related meme on the first page. This differs significantly from our perception of a “normal” meme (the memes of the early 2010s) with an image and a short blurb of text that is supposed to invoke laughter.
Memes have become a sort of coping mechanism for GenZ, as we have resorted to joking about and creating memes about problems such as war, climate change, and depression. The major difference between old school and GenZ memes is that GenZ has found out they can use memes to joke about “bad’ things. I think all the other memes are still similar to old memes in that they express ideas through pictures and simple words that are usually meant to be humorous. Memes have evolved and even have real-world implications. This was shown in the recent events where Reddit users or more specific users from a Reddit Community named “WallStreetBets” pushed up the stock value of Gamestop by more than 1000 percent in just a week by encouraging other Reddit users to buy the stock through––you guessed it––memes. Although memes may seem silly, they have shown countless times that they play a crucial role in disseminating information and popular culture in our day and age.
Dec 11, 2020 | Fun, Monica Chan
By Monica Chan (VI)
English 9: Angsty freshmen reading about other angsty freshmen.
English 10: No one actually read Jane Eyre.
Advanced Algebra and Trigonometry Honors: You thought you were good at math, didn’t you…oh well…
AP Statistics: Dear Ms. Peake, can you send me the entire Upper School student email list? I need to do another survey.
Math 6: https://www.wolframalpha.com.
Any Mr. Poprik class: “Ok Folks!”
Any Computer Science Class: The Labs and Problem Sets will bring my grade up, right?
AP US History: More like APUSH me off a cliff please.
US Environmental History Honors: Why didn’t I sign up for APUSH?
American Society and Culture: Boy, am I glad I didn’t sign up for APUSH.
Art Fundamentals: Wait, I thought this was supposed to be an easy graduation requirement!
Chemistry I: Colorado PhET.
AP Chemistry: A 70% curves to an A, right?
Honors Biology II: Were the Bio I Honors Projects not enough of a deterrent for you?
AP Physics C: Mechanics: Everything you learned last year, but add the word “derivative.”
AP Physics C: Electricity and Magnetism: Math 7.
Apr 20, 2020 | Fun, School News, Uncategorized
On February 3rd and 4th, sophomores and juniors participated in the preliminary round of the 2020 Robert H. Lebow Oratorical Competition. While the student body had the opportunity to watch the six finalists in the all-school assembly, they did not have the chance to hear all of the contestants perform their speeches and listen to their stories. All of the messages presented by the participants are important to the community, and as a result, excerpts from a few first-round speeches have been provided.
Brian Li: “The Neglect of Humanities in the 21st Century”
The humanities serve as the foundation for human civilization. They teach us how to think critically and creatively. They facilitate empathy and compassion. We communicate more clearly, understand cultural values, and are introduced to new perspectives through the humanities. Humanistic education has been the core of liberal arts since the ancient Greeks, challenging students through art, literature, and politics. The humanities bring clarity to the future by reflecting on the past. Perhaps most importantly, they allow us to explore and understand what it means to be human. We need, now more than ever, to be able to understand the humanity of others. And while STEM is undoubtedly beneficial for humankind, we cannot sustain the neglect of the humanities for much longer without suffering severe consequences. With revolutionary technology like AI and genetic engineering, the humanities are essential to ensure that we progress ethically and morally together.
Andrew Wong: “Where do you see yourself in 10 years?”
A question many of us in this room have heard in countless interviews, and yet it is a question that can reveal so much about ourselves. So, where will we be in 10 years? In 10 years, we will have found ourselves going through the entire college process and graduating from Pingry. We will go to and then graduate from college. We will have the rest of our lives splayed out in front of us, ready to grasp in our hands, as we enter the real world, ready to be the next generation of business people, engineers, doctors, lawyers, politicians, world leaders, and so much more. That answer seems pretty easy and straightforward, right? In reality, not so much.
Lauren Drzala: “An Uphill Battle”
As time went by, I was falling behind on work because I could not write at all, leaving me frustrated in school. In addition, my mental health was at an all-time low. I began to isolate myself, believing that no one could really understand how I was feeling. It was like I was falling and no one was there to catch me. On top of that, I was told I could not play my sport this winter, nor could I play the piano, an instrument that I have been playing since I was nine. I felt out of control and just had to watch the train wreck happen. I thought my friends had moved on so I tried to as well, but I just felt stuck. Left behind. I was in this mind set for a while, but it wasn’t until I realized that I could not give up on myself and settle for this empty feeling that my life started getting back on track. This triggered an uphill battle to try and climb my way out of the dark.
Aneesh Karuppur: “Straying from the Tune”
We are always told that “small steps will lead you to your goal” and “you won’t even know how much effort it really takes if you do it one step at a time.” But people forget that for this advice to work, you have to actually be looking at your feet and making sure that every step is in the right direction. Otherwise, you simply aren’t going to notice until you’re too far away from your goal to make a correction.
Apr 19, 2020 | Fun, Noah Bergam
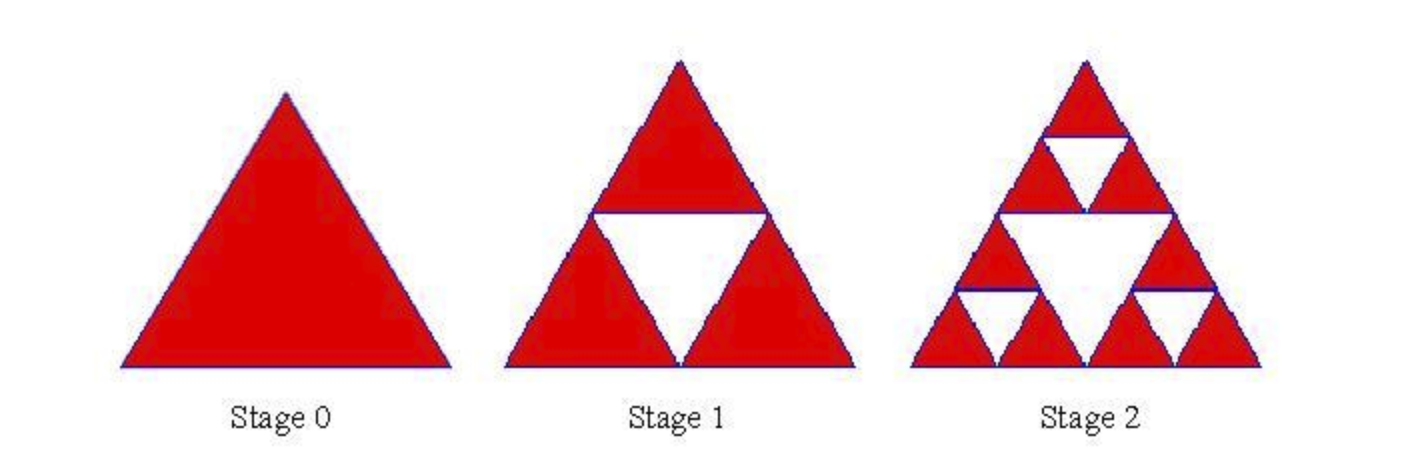
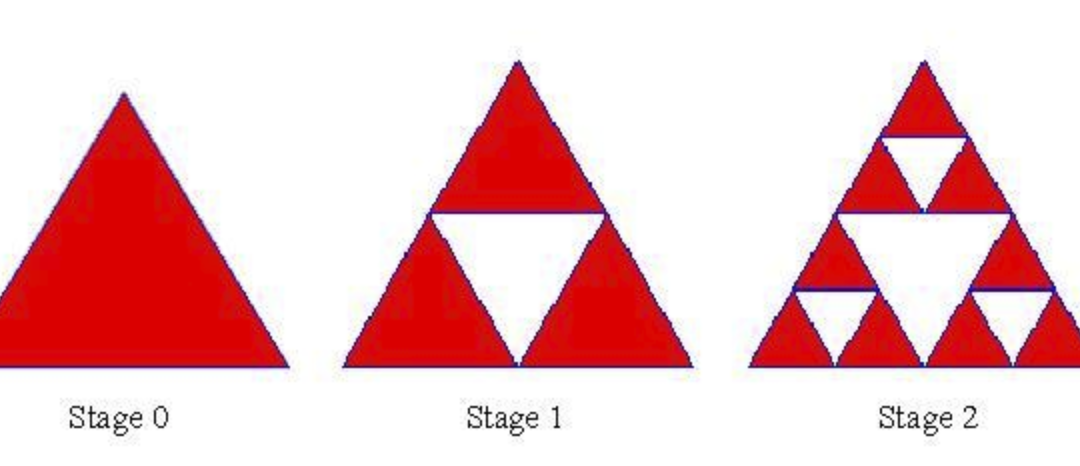
Fractals are self-similar. The Sierpinski Triangle is an interesting fractal pattern. You can build one like this:
- 1. Start with an “upright” equilateral triangle (as seen in stage zero)
- 2. Place an upside-down triangle in the center of any upright triangle
- 3. Repeat Step 2 infinitely
Write a recursive formula that can model how many similar triangles you can count in the figure in a given stage. The figure above will be helpful in finding the pattern.
Extra Challenge: Turn that recursive formula into an explicit formula (i.e. find S(n), where n is the “stage” and S(n) is the number of triangles)
Click for Solutions!
S(0) = 1
S(n) = 3S(n-1) + 2
Base case is 1 because there is only 1 triangle in Stage 0.
Look at the jump from stage 0 to 1. When you add the white triangle, you essentially have 3 smaller versions of Stage 0, along with the central triangle and the entire triangle. That’s 3*1+1+1.
Stage 1 to 2 follows the same pattern. 3(4) + 1 + 1.
Generalize the pattern to obtain your recursive step, S(n) = 3S(n-1) + 2.
—
In order to make an explicit formula, try expanding the recursive step.
S(n) = 3S(n-1) + 2
Replace S(n-1)
S(n) = 3( 3S(n-2) + 2 ) + 2
Replace S(n-2)
S(n) = 3( 3( 3S(n-3) + 2) + 2 ) + 2
Simplify to make the pattern more clear.
S(n) = 3^3 * S(n-3) + 18 + 6 + 2
If you keep on replacing k times you find the pattern:
S(n) = 3^k * S(n-k) + 2 + 6 + 18 + … 2*3k-1
We can get rid of S(n-k) by using our base case of S(0). When k=n, S(n-k) is 0. Thus…
S(n) = 3^n * S(0) + 2 + 6 + 18 + … 2*3n-1
Final Answer:
S(n) =3^n + ( 2+6 + 18 + … 2*3^(n-1) )
Or more formally, using sigma notation:
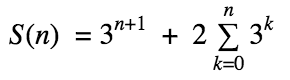

Apr 18, 2020 | Fun
Click for Solutions!
Across
2. Honohan 4. Jolly 8. Crowleydelman 10. Dunbar
Down
1. Grant 3. Horesta 5. Leone 6. Decatur 7. Jenkins 9. Trem
Apr 18, 2020 | Fun, Noah Bergam
In these confusing times there’s a certain sense of power that comes with understanding, or at least trying to understand, the dynamics of disease spread and epidemiology. I certainly felt that as I’ve looked into the mathematics disease modeling over the course of this quarantine––a field that is absolutely fascinating, empowering, and daunting all at once. I recommend checking out Julian Lee’s article on his original disease modeling application, which describes the effects of visiting friends in a quarantine (his application is a randomized agent-based model as opposed to the more top-down mathematical models you’ll see here).
In this article, I present three epidemiology thinking problems, in ascending orders of difficulty, meant to put you in the position of the disease modeler. Have fun!
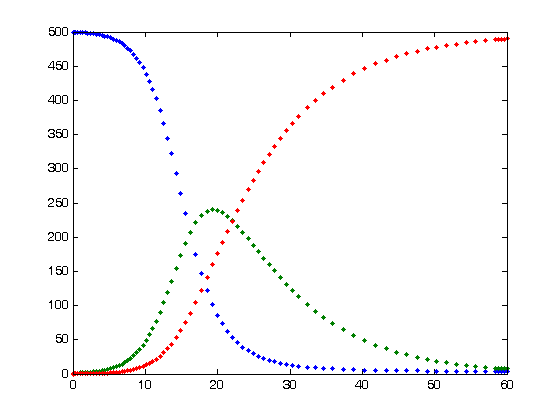
Fig: A graphical representation of an SIR (Susceptible-Infected-Recovered) Disease Model. The green curve is the curve that our social distancing efforts are “flattening.” This is the classic, top-down disease modeling approach
1) In epidemiology, R0 (“the basic reproductive number” or “r-naught”) is defined as the maximum number of new cases expected per infected person. The R0 of COVID-19 has been estimated to be 2.28 (Zhang, et al). An infected individual is expected to cause ß new cases per day. This is essentially the “birth rate.” Meanwhile, δ is the expected proportion of cases dying on a given day. This is essentially the “death rate.” Describe R0 in terms of ß and δ.
2) Does R0 tend to decrease, increase, or remain the same as a virus grows in an isolated population? Why or why not?
3) Consider the following differential equation to describe the spread of COVID-19, where ß and δ have the same values defined in problem 1.
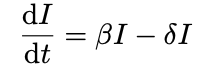
This is essentially a fancy mathematical way of saying that the rate at which the infection spreads is dependent on the number of people infected as well as the difference between the virus’ birth and death rates. In what ways does this model oversimplify real-life disease spread?
(Problems inspired by Rob J. de Boer’s Modeling Population Dynamics: a Graphical Approach, available here: http://theory.bio.uu.nl/rdb/books/mpd.pdf)
Click for Solutions!
1) R0 = ß/δ (1/δ is the mean number of days someone with the virus is expected to live.)
2) R0 decreases; as an infection grows, there will be more infected individuals around a given infected person, meaning that there are fewer people to infect.
3) There are a lot of answers to this question, which highlights the limitations of this top-down mathematical modeling. Here are a few.
- The ß value should not apply only to the infected population, but also to the healthy susceptible population.
- This model does not take into account the recovery rate.
- The virus’ birth rate will change, not only depending on the number of people with COVID but also depending on how well the population responds (social distancing, hand-washing, etc)
- The death rate will change based on what treatments are available.