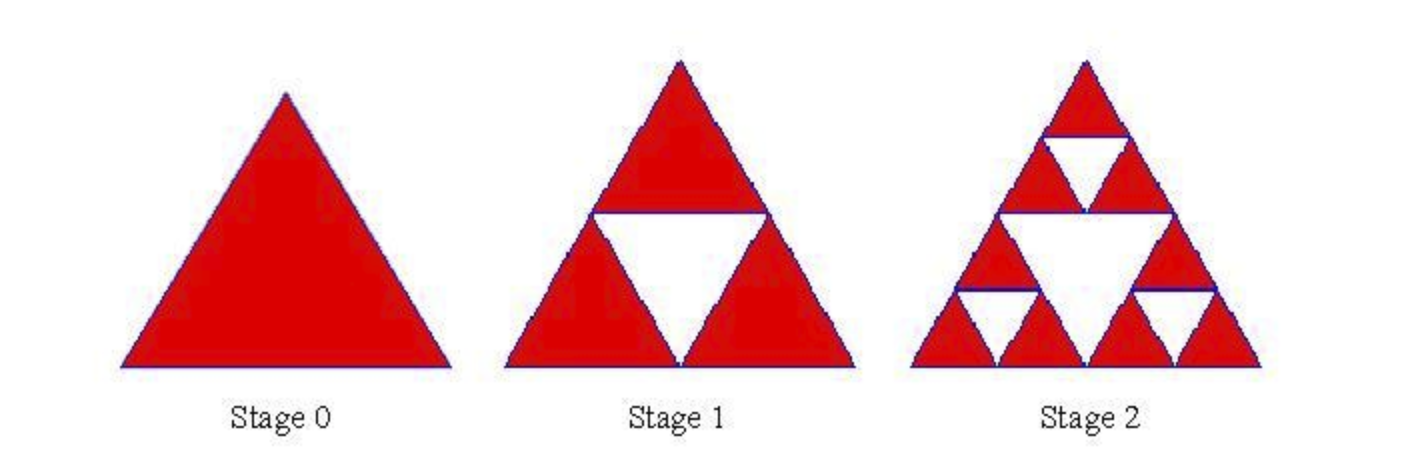
Fractals are self-similar. The Sierpinski Triangle is an interesting fractal pattern. You can build one like this:
- 1. Start with an “upright” equilateral triangle (as seen in stage zero)
- 2. Place an upside-down triangle in the center of any upright triangle
- 3. Repeat Step 2 infinitely
Write a recursive formula that can model how many similar triangles you can count in the figure in a given stage. The figure above will be helpful in finding the pattern.
Extra Challenge: Turn that recursive formula into an explicit formula (i.e. find S(n), where n is the “stage” and S(n) is the number of triangles)
Click for Solutions!
S(0) = 1
S(n) = 3S(n-1) + 2
Base case is 1 because there is only 1 triangle in Stage 0.
Look at the jump from stage 0 to 1. When you add the white triangle, you essentially have 3 smaller versions of Stage 0, along with the central triangle and the entire triangle. That’s 3*1+1+1.
Stage 1 to 2 follows the same pattern. 3(4) + 1 + 1.
Generalize the pattern to obtain your recursive step, S(n) = 3S(n-1) + 2.
—
In order to make an explicit formula, try expanding the recursive step.
S(n) = 3S(n-1) + 2
Replace S(n-1)
S(n) = 3( 3S(n-2) + 2 ) + 2
Replace S(n-2)
S(n) = 3( 3( 3S(n-3) + 2) + 2 ) + 2
Simplify to make the pattern more clear.
S(n) = 3^3 * S(n-3) + 18 + 6 + 2
If you keep on replacing k times you find the pattern:
S(n) = 3^k * S(n-k) + 2 + 6 + 18 + … 2*3k-1
We can get rid of S(n-k) by using our base case of S(0). When k=n, S(n-k) is 0. Thus…
S(n) = 3^n * S(0) + 2 + 6 + 18 + … 2*3n-1
Final Answer:
S(n) =3^n + ( 2+6 + 18 + … 2*3^(n-1) )
Or more formally, using sigma notation:
![]()
